Skip to main content

Mid Point Circle Drawing Derivation

Mid Point Circle Drawing Derivation (Algorithm)
The mid point circle algorithm is used to determine the pixels needed for rasterizing a circle while drawing a circle on a pixel screen.
In this technique algorithm determines the mid point between the next 2 possible consecutive pixels and then checks whether the mid point in inside or outside the circle and illuminates the pixel accordingly.



This is how a pixel screen is represented:
pixel representation on computer screen
A circle is highly symmetrical and can be divided into 8 Octets on graph. Lets take center of circle at Origin i.e (0,0) :
Mid Point Circle Drawing Derivation Algorithm
We need only to conclude the pixels of any one of the octet rest we can conclude because of symmetrical properties of circle.


Let us Take Quadrant 1: 
quadrant of mid point circle algorithm

Radius = OR = r
Radius = x intercept = y intercept
At point R
     coordinate of x = coordinate of y   or we can say  x=y
let us take Octet 2 of quadrant 1
here first pixel would be (0,y)
            here value of y intercept = radius (r)
 as circle’s center is at origin

         DERIVATION
Derivation of mid point circle drawing algorithm
let us assume we have plotted Pixel P whose coordinates are  
Now we need to determine the next pixel. 

We have chosen octet 2 where circle is moving forward and downwards so y can never be increased, either it can be same or decremented. Similarly x will always be increasing as circle is moving forward too.

So y is needed to be decided.
Now we need to decide whether we should go with point N or S.

For that decision Mid Point circle drawing technique will us decide our next pixel whether it will be N or S.

As 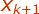  is the next most pixel of 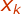  therefore we can write,

                    

And similarly 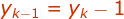  in this case.

Let M is the midpoint between 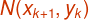  and .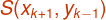 
And coordinates of point (M) are
                        Mid point Circle formula

                                  Formula of mid point circle


                                 final formula of mid point circle algorithm

Equation of Circle with Radius r

(x– h)2 + (y – k)2 = r2

When coordinates of centre are at Origin i.e., (h=0, k=0)

     x2 + y2 = r2    (Pythagoras theorem)
Function of Circle Equation

F(C) =  x2 + y2 - r2
Function of Midpoint M (xk+1 ,  yk -1/2) in circle equation

F(M)= xk+12 + (yk -1/2)2 - r2 
          = (xk+1)2 + (yk -1/2)2 - r2 

The above equation is too our decision parameter pk

Pk = (xk+1)2 + (yk -1/2)2 - r2           …….(i)

To find out the next decition parameter we need to get Pk+1

Pk+1 = (xk+1+1)2 + (yk+1 -1/2)2 - r2

Now,
Pk+1- Pk =  (xk+1+1)2 + (yk+1 -1/2)2 - r2
                          -[(xk+1)2 + (yk -1/2)2 - r2]

                     =  ((xk+1)+1)2 + (yk+1 -1/2)2
                            - (xk+1)2   - (yk -1/2)2 

                 = (xk+1)2 + 1 +2(xk+1) + yk+12 +(1/4) - yk+1
                      - (xk+1)2   - yk2 – (1/4) + yk+1

                = 2(xk+1) + yk+12 - yk2 - yk+1 + yk +1

                =  2(xk+1) +( yk+12 - yk2 ) - (yk+1 - yk) +1


Pk+1 = Pk + 2(xk+1)+( yk+12 - yk2 ) - (yk+1 - yk) +1     …..(ii)


Now let us conclude the initial decision parameter
For that we have to choose coordinates of starting point i.e. (0,r)
Put this in (i) i.e. Pk
Pk = (xk+1)2 + (yk -1/2)2 - r2
P0 = (0+1)2 + (r -1/2)2 - r2
        = 1 + r2 + ¼ - r – r2
        = 1 + ¼ - r

               …..(initial decision parameter)

Now If Pk ≥ 0 that means midpoint is outside the circle and S is closest pixel so we will choose S (xk+1,yk-1)
That means yk+1 = yk-1
Putting coordinates of S in (ii) then,

Pk+1 = Pk + 2(xk+1)+( yk-12 - yk2 ) - (yk-1 - yk) +1
        = Pk + 2(xk+1)+( yk -1)2 - yk2 ) - ((yk-1) - yk) +1
        = Pk + 2(xk+1)+yk 2+1-2yk - yk2 - yk+1 + yk +1
        = Pk + 2(xk+1)-2yk +2 + 1
        = Pk + 2(xk+1)-2(yk -1) + 1

As we know (xk+1 = xk+1) and (yk-1 = yk-1)
Therefore,
                Pk+1 = Pk + 2xk+1 - 2yk-1 + 1

And if Pk < 0 that means midpoint is inside the circle and N is closest pixel so we will choose N (xk+1 , yk)
i.e. yk+1 = yk
        Now put coordinates of N in (ii)
Pk+1 = Pk + 2(xk+1)+( yk2 - yk2 ) - (yk - yk) +1
        = Pk + 2(xk+1)+( yk2 - yk2 ) - (yk - yk) +1
        = Pk + 2(xk+1) +1

as xk+1 = xk+1 , therefore,
                        Pk+1 = Pk + 2xk+1 +1


      Hence we have derived the mid point circle drawing algorithm.





                               








Labels:

Comments

Post a Comment

Popular posts from this blog

Interactive Vs Non-Interactive Graphics

There are 2 types of Computer Graphics                     Interactive: Here user can engage with graphics i.e. it is two way communication between user and graphics. example : video games Non-Interactive: Here user cannot engage with graphics. It is one way communication user can only watch graphical activity without any interaction. example : TV broadcasting Interactive Graphics    Non-Interactive graphics      User interaction is required     The user has full control over     the  content                                                     Programmed in a way that user can   control   graphic    Examples :       Simulators (training pilots)       Video games       User Interface           User interaction is not required     The user only has control over     some parts  of   the content     Passive, totally controlled by     the Program  Examples:     Videos, m
5 comments
Read more

Bresenham's Line Drawing Derivation

Bresenham's Line Drawing Algorithm Derivation Bresenham Line drawing algorithm is used to determine closest points to be illuminated on the screen to form a line. As we know a line is made by joining 2 points, but in a computer screen, a line is drawn by illuminating the pixels on the screen. (Here pixel (1,2), (3,1) and (5,5) are illuminated and others are non-illuminated) A line from pixel (2,2) to (7,5) will be shown like this on the screen. The slope of a line plays a major role in the line equation that's why Bresenham line drawing algorithm calculates the equation according to the slope of the line. The slope of the line can be greater than 1 (m>1) or less than or equal to 1 (m<=1). Now enough talking let's derive the equations. Derivation: Let's say we want to draw a line on the screen. so, to draw a line we have to calculate the points or pixels to be illuminated on the screen. Now while drawing a line a som
9 comments
Read more

Bresenham's Circle Drawing Derivation

Bresenham's Circle Drawing Algorithm Derivation Bresenham circle drawing algorithm is used to determine the next pixel of screen to be illuminated while drawing a circle by determining the closest nearby pixel. Let us first take a look how a circle is drawn on a pixel screen (this is how pixel graph is represented) As Circles are symmetrical so the values of y-intercept and x-intercept are are same if circle's Center coordinates are at Origin (0,0). Here,  Radius = OA = r Due to symmetrical property of Circle we don't need to calculate all the pixels of all the octets and quadrants We need to find the pixels of only one octet, rest we can conclude through this. Lets take the Octet 2 which is in quadrant 1 here both x and y are positive here the initial pixel would be (0,y) coordinate At point R both the value of both x and y coordinates would be same as R is at same distance of Both X and Y axis.
7 comments
Read more