Bresenham's Circle Drawing Derivation

Bresenham's Circle Drawing Algorithm Derivation

Bresenham circle drawing algorithm is used to determine the next pixel of screen to be illuminated while drawing a circle by determining the closest nearby pixel.

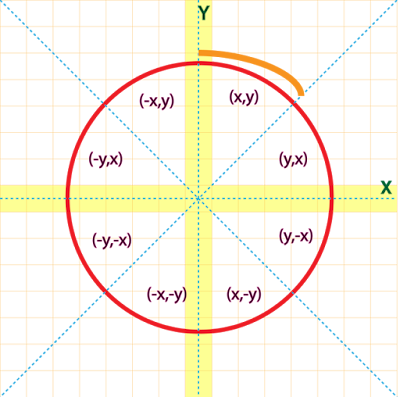
Let us first take a look how a circle is drawn on a pixel screen

(this is how pixel graph is represented)

As Circles are symmetrical so the values of y-intercept and x-intercept are

are same if circle's Center coordinates are at Origin (0,0).

Here,

 Radius = OA = r

Due to symmetrical property of Circle we don't need to calculate all the pixels of all the octets and quadrants

We need to find the pixels of only one octet, rest we can conclude through this.

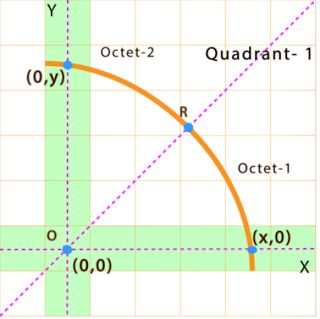
^{Lets take the Octet 2 which is in quadrant 1}

here both x and y are positive

here the initial pixel would be (0,y) coordinate

^{At point R both the value of both x and y coordinates would be same as R is at same distance of Both X and Y axis.}

Derivation of Bresenham circle algorithm: 

Let's say our circle is at some random pixel P whose coordinates are (x_k, y_k).

Now we need to find out our next pixel.

Note- This is octet 2 so here x can never be decremented as per properties of a circle but y either needs to decremented or to be kept same. y is needed to be decided.

Here it needs to decide whether go with N or S.

For this bresenham's circle drawing algorithm will help us to decide by calculating the difference between radius and the coordinates of the next pixels.

The shortest of d1 and d2 will help us Decide our next pixel.

note-       x_k+1 = x_k +1 

                              As  x_k+1  is the next consecutive pixel of x_k

similarly

             y_k-1 = y_k -1

  

Equation of Circle with Radius r

(x– h)² + (y – k)² = r²

When coordinates of centre are at Origin i.e., (h=0, k=0)

     x² + y² = r²    (Pythagoras theorem)

Function of Circle Equation

F(C) = x² + y² - r²

Function of Circle at N

             F(N) = (x_k+1)² + (y_k)² – r²            (Positive)

Here the value of F(N) will be positive because N is out-side the circle

that makes  (x_k+1)² + (y_k)²  Greater than r²

Function of Circle at S

             F(S) = (x_k+1)² + (y_k-1)² – r²          (Negative)

Here the value of F(S) will be Negative because S is  in-side the circle that makes (x_k+1)² + (y_k-1)²  Less than r²

Now we need a decision parameter which help us decide the next pixel

      Say D_k

               And ,   D_k = F(N)+F(S)

Here either we will get the positive or negative value of D_k

So if D_k < 0

              that means the negative F(S) is bigger then the positive F(N), that implies Point N is closer to the circle than point S. So we will select pixel N as our next pixel.

and if   D_k > 0

              that means positive F(N) is bigger and S is more closer as F(S) is  smaller. So we will Select S as our next pixel.

Now lets find  D_k

          D_k  =  (x_k+1)² + (y_k)² – r²   +  (x_k+1)² + (y_k-1)² – r²

                                                      (replacing x_k+1 with x_k + 1 and y_k-1 with y_k -1)

                = (x_k + 1)² + (y_k)² – r²   +  (x_k + 1)² + (y_k -1)² – r²

                = 2(x_k + 1)² + (y_k)²  + (y_k -1)² – 2r²            ----- (i)

Now lets find D_k+1

(Replacing every k with k+1)

       D_k+1 = 2(x_k+1 + 1)² +(y_k+1)²  + (y_k+1 -1)² – 2r²

             = 2(x_k+1 + 1)² + (y_k+1)²  + (y_k+1 -1)² – 2r²

(Replacing  x_k+1  with  x_k + 1   but now we can’t replace  y_k+1 because we don’t know the exact value of y_k )

              = 2(x_k+1+ 1)² + (y_k+1)²  + (y_k+1 -1)² – 2r²

                             = 2(x_k+2)² + (y_k+1)²  + (y_k+1 -1)² – 2r²          ----- (ii)

  

Now to find out the decision parameter of next pixel i.e. D_k+1

We need to find

       D_k+1 - D_k = (ii) - (i)

        = 2(x_k+2)² + (y_k+1)²  + (y_k+1 -1)² – 2r²

                       - [ 2(x_k + 1)² + (y_k)²  + (y_k -1)² – 2r²]

        =    2(x_k)² + 8x_k + 8 + (y_k+1)² + (y_k+1)² - 2y_k+1 + 1 - 2r²

     - 2x_k  - 4x_k – 2  - (y_k)²  - (y_k)² + 2y_k  - 1  + 2r²

        =  4x_k + 2(y_k+1)²  - 2y_k+1  - 2(y_k)² - 2y_k + 6

D_k+1 = D_k + 4x_k + 2(y_k+1)²  - 2y_k+1  - 2(y_k)² - 2y_k + 6       ----- (iii)

If (D_k < 0) then we will choose N point as discussed.

i.e. (x_k+1, y_k)

that means our next x coordinate is x_k+1 and next y coordinate is y_k i.e. y_k+1 = y_k, putting y_k in (iii) in replace of y_k+1

now,

       D_k+1 = D_k + 4x_k + 2(y_k)²  - 2y_k  - 2(y_k)² - 2y_k + 6     

   

=  D_k + 4x_k + 6

If (D_k > 0) then we will choose S point.

i.e. (x_k+1, y_k-1)

that means our next x coordinate is x_k+1 and next y coordinate is y_k i.e. y_k+1 = y_k-1 putting y_k-1 in (iii) in replace of y_k+1

now,

          D_k+1 = D_k + 4x_k + 2(y_k-1)²  - 2y_k-1  - 2(y_k)² - 2y_k + 6

Now we know

y_k-1 = y_k – 1

therefore,

D_k+1 = D_k + 4x_k + 2(y_k -1)²  - 2(y_k -1)  - 2(y_k)² - 2y_k + 6

          = D_k + 4x_k + 2(y_k) ² + 2 - 4y_k  - 2y_k +2  - 2(y_k)² - 2y_k + 6

     = D_k + 4x_k - 4y_k + 10

        = D_k + 4(x_k - y_k) + 10

Now to find initial decision parameter means starting point that is (0,r) ,value of y is r

Putting (0,r) in (i)

D_k = 2(x_k + 1)² + (y_k)²  + (y_k -1)² – 2r²

D₀ = 2(0 + 1)² + r²  + (r -1)² – 2r²

     = 2 + r² +r² + 1 – 2r – 2r²

       = 3-2r

Hence we have derived the bresenham’s Circle drawing technique.

More>>

Bresenham circle drawing algorithm 
Bresenhams Circle drawing program in C 
Bresenhams line drawing derivation 
Bresenhams Line drawing program in C 
Mid point circle drawing algorithm's derivation 
What is computer graphics