Bresenham's Line Drawing Algorithm Derivation
A line from pixel (2,2) to (7,5) will be shown like this on the screen.
The slope of a line plays a major role in the line equation that's why Bresenham line drawing algorithm calculates the equation according to the slope of the line.
The slope of the line can be greater than 1 (m>1) or less than or equal to 1 (m<=1).
Now enough talking let's derive the equations.
Derivation:
Let's say we want to draw a line on the screen.
so, to draw a line we have to calculate the points or pixels to be illuminated on the screen.
Now while drawing a line a sometimes it passes through 2 pixels at the same time then we have to choose 1 pixel from the 2 to illuminate it.
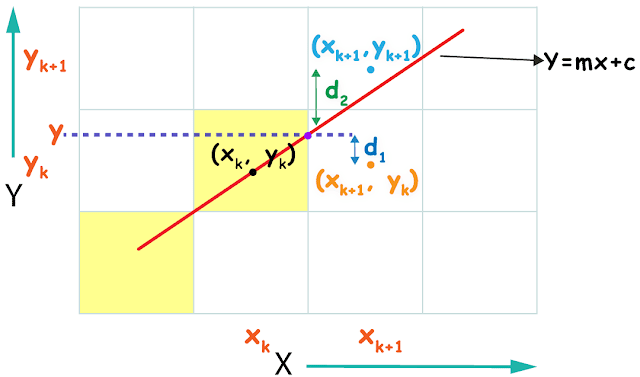
so, the bresenham algorithm calculates the distance from the intersection point y to both the pixels and whichever is smaller we choose that pixel.
The equation of Line is:
First we calculate the slope of the line if slope is less than 1, then X will always be incremented.
so at (m<=1)
we calculate the d1 which is distance between intersection point y to the pixel yk
Bresenham Line drawing algorithm is used to determine closest points to be illuminated on the screen to form a line.
As we know a line is made by joining 2 points, but in a computer screen, a line is drawn by illuminating the pixels on the screen.
As we know a line is made by joining 2 points, but in a computer screen, a line is drawn by illuminating the pixels on the screen.
(Here pixel (1,2), (3,1) and (5,5) are illuminated and others are non-illuminated)
The slope of a line plays a major role in the line equation that's why Bresenham line drawing algorithm calculates the equation according to the slope of the line.
The slope of the line can be greater than 1 (m>1) or less than or equal to 1 (m<=1).
Now enough talking let's derive the equations.
Derivation:
so, to draw a line we have to calculate the points or pixels to be illuminated on the screen.
Now while drawing a line a sometimes it passes through 2 pixels at the same time then we have to choose 1 pixel from the 2 to illuminate it.
so, the bresenham algorithm calculates the distance from the intersection point y to both the pixels and whichever is smaller we choose that pixel.
The equation of Line is:
Y=mx+c ....(1)
Here m is the slope of Line and
C is y-Intercept of line
The slope can also be written as
so at (m<=1)
we calculate the d1 which is distance between intersection point y to the pixel yk
So, d1 = y-yk
d1 = mxk+1 +c -yk By using ....(1)
Similarly d2 is the distance between pixel yk+1 and intersection point y.
d2 = yk+1-y
d2 = yk+1-(mxk+1+c) By using ....(1)
Note: here x is always incrementing so we can write xk+1 as xk +1 and here yk+1 is next pixel so we can write it as yk+1.
subtracting d2 from d1
d1-d2 = m(xk+1) +c -yk – [yk+1-(mxk+1+c)]
= m(xk+1)+c -yk – yk-1+m(xk+1)+c
d1-d2 = 2m(xk+1)-2yk+2c-1 .....(3)
d1 = mxk+1 +c -yk By using ....(1)
Similarly d2 is the distance between pixel yk+1 and intersection point y.
d2 = yk+1-y
d2 = yk+1-(mxk+1+c) By using ....(1)
Note: here x is always incrementing so we can write xk+1 as xk +1 and here yk+1 is next pixel so we can write it as yk+1.
subtracting d2 from d1
d1-d2 = m(xk+1) +c -yk – [yk+1-(mxk+1+c)]
= m(xk+1)+c -yk – yk-1+m(xk+1)+c
d1-d2 = 2m(xk+1)-2yk+2c-1 .....(3)
Multiplying both side by (dx)
dx(d1-d2) = 2dy(xk+1)-2dx(yk)+2dx(c)-dx
Now we need to find decision parameter PK
PK= dx(d1-d2) and,
C = 2dy+2dx(c)-dx which is constant
So new equation is.
PK =2dy(xk)-2dx(yk) +C .......(4)
Now our next parameter will be
PK+1 =2dy(xk+1)-2dx(yk+1) +C .....(5)
Subtracting Pk from PK+1
Pk+1-Pk= 2dy(xk+1-xk)-2dx(yk+1-yk) +C-C
Note: here x is always incrementing so we can write xk+1 as xk +1
Pk+1-Pk= 2dy(xk-xk+1)-2dx(yk+1-yk)
Pk+1 = Pk+2dy-2dx(yk+1-yk)........(6)
when Pk<0 then (d1-d2)<0
So d1<d2 then we will write yk+1 as yk because current pixel’s distance from intersection point y is smaller.so, we will have to choose current pixel.
Then our formula will be:
Pk+1 = Pk+2dy-2dx(yk-yk)
Pk+1 = Pk+2dy
And when Pk>0 then (d1-d2)>0
So d1>d2 then we will write yk+1 as yk+1 because current pixel’s distance from intersection point y is larger.so, we will have to choose upper pixel.
At that time our formula will be:
Pk+1 = Pk+2dy-2dx(yk+1-yk)
Pk+1 = Pk+2dy-2dx
We can say that (yk+1-yk) value can either be 0 or 1.
For Initial decision parameter
From 4th equation
PK = 2dy(xk)-2dx(yk) +C
PK = 2dy(xk)-2dx(yk)+2dx(c)-dx+2dy
By using 1st equation
yk=m(xk)+c
c=yk-m(xk)
P0 = 2dy(xk)-2dx(yk)+2dx(yk-m(xk)-dx (By using 2)
= 2dy(xk)-2dx(yk)+2dxyk-2dyxk+2dy-dx
P0 =2dy-dx
But if the slope of line is greater then 1 (m>1).
then our Y coordinate will always be incremented and we have to choose between xk or xk+1.
So, our Line equation will be:
Yk+1 = m(x)+c
Now, In this case our d1 will be the distance between intersection point x and pixel xk
d1= x-xk By using ....(7)
d1= 1/m(yk+1-c)-xk
And similarly our d2 will be the distance between intersection point x and pixel xk+1
d2 = xk+1-x By using ....(7)
d2 = xk+1-1/m(yk+1-c)
Note: here y is always incrementing so we can write yk+1 as yk+1 and here xk+1 is next pixel so we can write it as xk+1.
subtracting d2 from d1
d1-d2 =1/m(yk+1-c)-xk – [xk+1-1/m(yk+1-c)]
= 1/m(yk+1-c)-xk – xk-1+1/m(yk+1-c)
d1-d2 = 2/m(yk+1-c)-2xk-1
d1-d2 = 2dx(yk+1-c)-2dyxk-dy
Multiplying both side by (dy)
dy(d1-d2) = 2dxyk+2dx-2dxc-2dyxk-dy
Now we need to find decision parameter PK
PK = dy(d1-d2)
C = 2dx-2dxc-dy which is constant
So new equation is
PK = 2dxyk-2dyxk +C ......(8)
Now our next parameter will be
Pk+1 = 2dx(yk+1)-2dy(xk+1)+C
Substracting Pk from Pk+1
Pk+1-Pk = 2dx(yk+1-yk)-2dy(xk+1-xk)+C-C
Note: here x is always incrementing so we can write yk+1 as yk +1
Pk+1-Pk = 2dx(yk +1-yk)-2dy(xk+1-xk)
Pk+1=Pk+2dx-2dy(xk+1-xk)
when Pk<0 then (d1-d2)<0
So d1<d2 then we will write xk+1 as xk because current pixel’s distance from intersection point x is smaller.so, we will have to choose current pixel.
Then our formula will be:
Pk+1 = Pk+2dx-2dy(xk-xk)
Pk+1 = Pk+2dx
And when Pk>0 then (d1-d2)>0
So d1>d2 then we will write xk+1 as xk+1 because current pixel’s distance from intersection point x is Larger.so, we will have to choose next pixel.
At that time our formula will be:
Pk+1= Pk+2dx-2dy(xk+1-xk)
Pk+1= Pk+2dx-2dy
For Initial decision parameter
From 8th equation
PK = 2dxyk-2dyxk +C
P0 = 2dxy0+2dx-2dxc-2dyx0-dy
By using 1st equation
yk=m(xk)+c
c=yk-m(xk)P0 = 2dxy0-2dyx0+2dx-2dx(y0-m(x0))-dy yk=m(xk)+c
P0 = 2dxy0-2dyx0+2dx-2dxy0+2dyx0-dy (By using 2)
P0 = 2dx-dy
hence formulas for bresenham is derived.



derivation part of bresenhams algorithm is high
ReplyDeleteVery nice and easily understandable .Thank uh
ReplyDeleteBest derivation for bresenham algo on internet AFAIK
ReplyDeletebest derivation ever
ReplyDeleteFor slope is negative
ReplyDeleteThank you
ReplyDeleteMy teacher is mad ��
But u explained it very well
Thanks a lot. It's so much easier to understand.
ReplyDelete:) :)
ok
ReplyDeleteVERY EASY AND SIMPLE TO UNDERSTAND EXPLANATION !!! THANK YOU SO MUCH
ReplyDelete